Общая характеристика школьных математических олимпиад. Примеры задач математических олимпиад для 7-9 классов
(A1A2B1B2)( A3B3C3)( C1C2C3)=(A1A2A3B1B2B3C1C2C3)C3.
1688=2С3. Откуда С3=512, A3B3=8/512=1/64.
Ответ: 1/64.
3. 
.
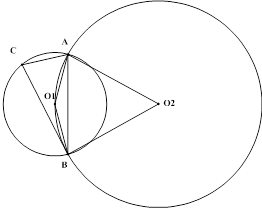
4.Пусть вписанный в первую окружность 
. Соответствующий ему центральный угол 
. Но 
вписан во вторую окружность, поэтому 
. 
- это угол между касательной BC и секущей AB, поэтому 
.
Тогда по теореме о сумме углов треугольника,
. Значит, 
- равнобедренный. AB=BC, что и требовалось доказать.
5. Каждому цвету поставим в соответствие один из остатков по модулю 4. Синий - 0, оранжевый - 1, фиолетовый - 2, зелёный - 3. Вместо хамелеонов будем рассматривать 2002 целых числа, стоящие по кругу. Операция смены цвета в новой трактовке будет равносильна прибавлению 1 к четырём последовательно стоящим числам. (При этом, если будет получаться число, большее 3, то оно заменяется на остаток от деления на 4.) В начальный момент времени по кругу стоят нули и нам требуется узнать, можно ли путём указанной операции сделать все числа, равные трём.
В начальный момент времени сумма равна 0 и на каждом шаге она может изменяться лишь на величину, кратную четырём, т.е. сумма всех чисел на каждом шаге будет делиться на 4. Поэтому 2002 тройки (которые в сумме дают 6006=41501+2) получить нельзя.
Материалы по педагогике:
Работа над усвоением словарных слов
В начальной школе программой по русскому языку предусмотрено обязательное изучение слов, правописание которых правилами не проверяется. Одной из главных задач, стоящих перед учителем, является задача научить ребенка писать эти слова без ошибок. Сделать процесс усвоения трудных слов более эффективны ...
Продолжительность различных видов работ педагога-психолога образования
№ Вид работы Среднее время, ч. Примечание 1 Создание плана работы 2,5 6,0 на месяц на год 2 Создание отчета про выполненную работу 4 8 на месяц на год 3 Индивидуальная психодиагностическая работа, подготовка к обследованию, его проведение и обработка результатов, оформление заключения и рекомендаци ...
Требования профессии к личности педагога
«Образ педагога» обсуждался во все времена, эта тема стала еще более актуальной сегодня, когда в России набирает обороты реформа образовательной системы. Государство и общество предъявляют школе большие требования. Грядут серьезные изменения. И в первую очередь должен меняться педагог. Современному ...