Этапы изучения алгоритма в школе

Ответ:

а=0 , а=-4 то хR;

, то;

, то .

Пример 8.

Ответ:

a<-2 а=2, то нет решения;

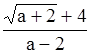а, то х < ;

, то х>.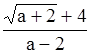

Примеры для самостоятельного решения:

1)2∙а∙х+5>а+10∙x;

2)a∙x+x+1 <0;

3)x+1≤a∙x+a2;

4)a∙x+16≤a2-4∙x;

5)m∙x>1+3∙x;

6);

7);

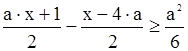8) (x-1) ∙ (a2-1)>5-4∙a;

9)b-3∙b+4∙b∙x<4∙b+12∙x;

Факультатив “Решение неравенств с параметром первой степени с одной неизвестной” был проведён в 9 классе в школе №52 г. Кирова. Цель данного факультатива была достигнута. Применение алгоритмического метода позволило сделать изложение данной темы более доступным, учащиеся научились решать линейные неравенства с параметром осознанно.

Заключение

В ходе исследования были решены следующие задачи:

1) Изучена учебно-методическая литература по применению алгоритмического метода в школе;

2) Рассмотрены следующие вопросы, связанные с алгоритмическим методом: история возникновения алгоритма; определение алгоритма, его свойства, основные этапы алгоритмического процесса и классификация алгоритмов.

3) Разработана методика формирования алгоритмов “Решение алгебраических неравенств 1 и 2 степени с одним неизвестным”.

4) Показано как алгоритмический метод может применяться при решении линейных неравенств с параметром на факультативном занятии.

Материалы по педагогике:

Технология развития мотивационных основ к урокам физической культуры
Одной из наиболее сложных структур личности является мотивирование. Поскольку мотив всегда рассматривался как основа деятельности, его формированию посвящали свои исследования практически все ученые педагоги и психологи. В исследованиях наших аспирантов (Бахтина О.В., Волощенко И.И., Г.Г. Лаптиева, ...

Использование пластико-ритмической гимнастики в воспитании детей с фонетико-фонематическим недоразвитием речи
В специальной литературе отмечается, что у многих детей с речевой патологией имеются отклонения в состоянии общей и тонкой моторики, а также наблюдаются особенности ее развития. В связи с этим авторы подчеркивают необходимость специальной работы по коррекции нарушений двигательной сферы у детей с р ...

Массовая внеклассная работа по химии
Массовая внеклассная работа по химии включает мероприятия, охватывающие не только учащихся, интересующихся химией, но и всех остальных. К таким мероприятиям относятся химические вечера, научно – практические и читательские конференции, химические олимпиады, дни, недели, месячники химии, экскурсии н ...