Этапы изучения алгоритма в школе

Ответ: а=1, то хR;

а= -1, то нет решения;

, то x ≤;

, то x .

Пример 4.

2а∙(а-2) ∙х а-2

1) 2а∙(а-2)=0 а=0 или а=2

а=0 х∙0-2 верно

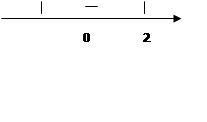а=2 х∙00 неверно

2) 2а∙(а-2)>0 а,

то х

3) 2а∙(а-2)<0 , то х

Ответ:

а=0, то хR;

а=2, то нет решения;

а, то х;

, то х.

Пример 5.

(а2-9) ∙ха+3

1) а2-9=0

а=3 и а=-3

а=3 0х6 верно;

а=-3 0х0 верно;

2) ;

3) ;

Ответ:

а=3 , а=-3 то хR;

, то;

, то ;

Пример 6.

а2х-а ∙х > a-1x∙ (a2-a) > a-1x∙(a∙ [a-1]) > a-1

a∙ [a-1]=0a=0 и а=1

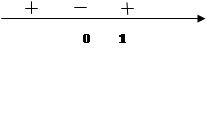а=0 0∙х>-1 верно

а=1 0∙х>0 неверно

2); х>

3)а; х<

Ответ:

а=0, то хR;

а=1, то нет решения;

a, то х>;

, то х<.

Пример 7.

а2∙х+4а∙х-а-4≤0

Материалы по педагогике:

Кружковые занятия по математике и методика её проведения
Математический кружок - одна из наиболее действенных и эффективных форм внеклассных занятий. В основе кружковой работы лежит принцип строгой добровольности. Обычно кружковые занятия организуются для хорошо успевающих учащихся. Однако следует иметь в виду, что иногда и слабо успевающие учащиеся изъя ...

Принципы целевого отбора текстов
Коммуникативно-прагматический подход к фактам языка, рассмотрение их в русле теории речевой деятельности, характерное для лингвистических и психологических исследований последних лет, представляется особенно плодотворным и перспективным для методики. И это не удивительно, поскольку основной задачей ...

Создание и развитие системы начального музыкального образования в г.Белгороде
С малых лет следует приучать ребенка усваивать красоту звука. Ребенок должен слушать прекрасную музыку и пение, его необходимо приобщать к музыкальной культуре, чтобы музыка стала его эстетической потребностью. Но сейчас музыка звучит разная, очень много музыки некачественной. Разобраться в ней пом ...