Этапы изучения алгоритма в школе

5.Решите неравенство методом интервалов.

1)

2)

3)

6.Решите неравенство.

1)

2)

3)

Опытное преподавание

Факультативное занятие в девятом классе (решение неравенств с параметром первой степени с одной неизвестной).

Цель:

применить алгоритмический метод при формировании умений и навыков в решении линейных неравенствах с параметрами.

Задачи:

расширить кругозор учащихся;

воспитание внимания, аккуратности, самостоятельности;

осуществление взаимосвязи теории и практики;

развитие памяти, логического мышления.

Решение задач с параметрами всегда вызывает большие трудности у учащихся. Причём часто учащиеся испытывают психологические трудности, «боятся» таких задач, так как не видят связи в их решении с решениями линейных неравенств с одной переменной.

Изучение линейных неравенств с параметром первой степени с одной неизвестной не возможно без умения решать линейные неравенства с одной переменной. Так как факультатив проводился в 9 классе, а линейные неравенства изучались в восьмом классе, то возникла необходимость актуализировать знания по решению линейных неравенств, вспомнить этапы их решения. Ученикам можно предложить следующее задание.

Решите неравенство 2(х+5)-3≥4+3х

Все решают у себя в тетрадях, а один ученик решает у доски. Запись ведёт в два столбика. Решение в одном столбика, а в другом записывают пояснения к своим действиям.

2х+7≥4+3х Раскрыли скобки в обеих частях неравенства

2х-3х≥4-2 Перенесли слагаемые, содержащие переменную в одну

часть, а не содержащую в другую.

-х≥2 Привели подобные члены в каждой части.

х≤-2 Разделили обе части неравенства на коэффициент при

переменной (учитывая его знак !).

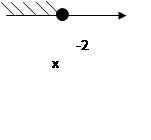Отметили соответствующие промежутки на

координатной прямой.

х(-∞;-2] Записали числовой промежуток

После того как повторили этапы решения линейных неравенств с одной переменной, учитель предлагает на доске подробный разбор решения неравенства с параметром. Затем ученики вместе с учителем формулируют алгоритм решения линейных неравенств с параметром.

Пример 1. Рассмотрим решение неравенства (а-4)∙х<12

Чтобы найти х, обе части неравенства хочется разделить на (а-4). Однако теперь важно положительно, отрицательно или равно нулю выражение (а-4).

Определим знак выражения

Рассмотрим три случая:

а-4=0

а-4>0

а-4<0

1)если а-4=0а=4, то неравенство примет вид 0х<12, которое справедливо для всех хR

2) a-4>0 a>4, то разделим обе части неравенства на положительное выражение (а-4), не меняя знак неравенства, получим х > (используем свойство числового неравенства).

Материалы по педагогике:

Анализ опытно-экспериментальной работы
Разрабатывая программу формирования культуры делового общения студентов, мы исходили из закономерностей развития и функционирования модели формирования культуры делового общения; собственная работа особенностей коммуникативной деятельности студентов; анализа существующей практики профессиональной п ...

Фундаментальные науки в системе высшего образования
Интеграция Болонского процесса в систему образования Украины принесла множество изменений. Первое и самое главное - внедрение независимого тестирования для школьников, а также упрощение системы уровней выпускников вузов. Но это только те изменения, которые видны для всех. На деле Болонский процесс ...

Учет гендерных особенностей в воспитательной работе
Воспитание, развитие мальчиков и девочек настолько различно, что можно сказать, что они растут в параллельных мирах. К сожалению каждый из нас живет в одном мире и нам не дано попасть в мир другого пола, пожить его проблемами, переживаниями, проникнуть в мир мыслей, понятий, отношений и негласных п ...