Этапы изучения алгоритма в школе

9. Сколько железнодорожных платформ потребуется для перевозки 183 контейнеров, если на одной платформе можно разместить не более 5 контейнеров.

10. Одна сторона треугольника равна 8 см., другая – 13см.

каким наименьшим целым числом сантиметров может быть длина третьей стороны?

каким наибольшим целым числом сантиметров может быть длина третьей стороны?

11.При каких значениях х точки графика функции у=3х+1.5 лежат выше точек графика функции у=-2х+1.

Формирование алгоритма « Решение неравенств второй степени с одним неизвестным»

Цель:

выработать умение решать неравенства второй степени с одним неизвестным и системы квадратных неравенств.

Решение квадратных неравенств – это традиционно обособленная часть исследования свойств квадратичной функции. Например, задача о решении неравенства х2-5х+6<0 может быть переформулирована в задачу о нахождении промежутков, на которых функция у =х2-5х+6 принимает отрицательные значения, а это легко решается с помощью эскиза графика. Этот способ фактически является строгим обоснованием графического способа.

Метод интервалов является логическим продолжением решения квадратных неравенств. Он позволяет решать более сложные неравенства, у которых левая часть – многочлен любой степень, представляемый в виде простых множителей, или дробь, у которой числитель и знаменатель также многочлены, разлагаемые на множители.

В результате изучения темы учащиеся должны уметь:

решать квадратные неравенства с одной неизвестной графически и методом интервалов

Специфические действия:

Привидение неравенства к квадратному виду.

Решение квадратных уравнений.

Построение графиков функций (схематично).

Выполнение тождественных преобразований.

Определение знака выражения на соответствующих промежутках.

Алгоритм решения квадратных неравенств с одной переменной.

«Ядерным» материалом темы является:

1. Понятия «< » , « > » неравенство, решение неравенства решение системы неравенств, равносильных неравенств;

2. Свойства числовых неравенств, равносильных неравенств;

3. Алгоритм решения квадратных неравенств с одной переменной и решения системы неравенств.

4. Свойства графика квадратичной функции.

Рассмотрим работу с алгоритмом решения неравенств второй степени (графически) поэтапно. На первом этапе полезно актуализировать знания: нахождение корней квадратного трёхчлена, дискриминанта, изображение графиков квадратичных функций (схематично). После этого формулируем сам алгоритм. На втором этапе отрабатываем отдельные операции, входящие в алгоритм: изображение графиков функций, нахождение при каких значениях х функция принимает положительные, а при каких отрицательные значения. На третьем этапе применяем алгоритм при решении более сложных задач.

I. Введение алгоритма.

Рассмотрим введение алгоритма “решение неравенств второй степени с одним неизвестным” (графическим методом) с использованием обучающих самостоятельных работ.

1.Актуализация знаний

Обучающую самостоятельную работу проводим по новому материалу,

но перед этим повторим ранее изученные понятия, которыми придётся воспользоваться.

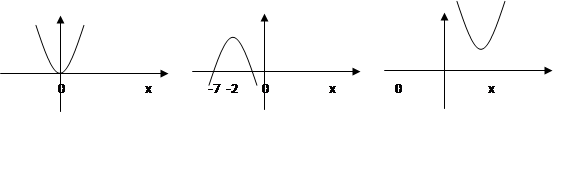1. у у у

а) Куда направлены ветви параболы?

b) Пересекает ли парабола ось ох, если да то сколько раз?

с) При каких х парабола принимает положительные значения?

d) При каких х парабола принимает отрицательные значения?

2. Изобразите схематично график функции.

Материалы по педагогике:

Работоспособность младших школьников
Работоспособность – это способность человека развить максимум энергии и, экономно расходуя её, достичь поставленной цели при качественном выполнении умственной или физической работы. Это обеспечивается оптимальным состоянием различных физиологических систем организма при их синхронной, скоординиров ...

Анализ результатов изучения нарушений произношения у дошкольников со стертой дизартрией
На основании проведенного обследования произносительной стороны речи у ребенка старшего дошкольного возраста со стертой формой дизартрии по методике О.Е.Грибовой выявлены следующие результаты Рис. 1 Результаты обследования Даниила З На Рис. 1 показано, что развитие произносительной стороны у обслед ...

Влияние обычаев и традиций на формирование личности
Формирование личности ребёнка, безусловно, включает и вопрос воспитания в ребёнке уважительного отношения к людям разных национальностей. Ребёнок с дошкольного возраста должен видеть в каждом из своих маленьких товарищей друга по взаимопомощи, по духу. У каждого человека имеется своеобразная, специ ...