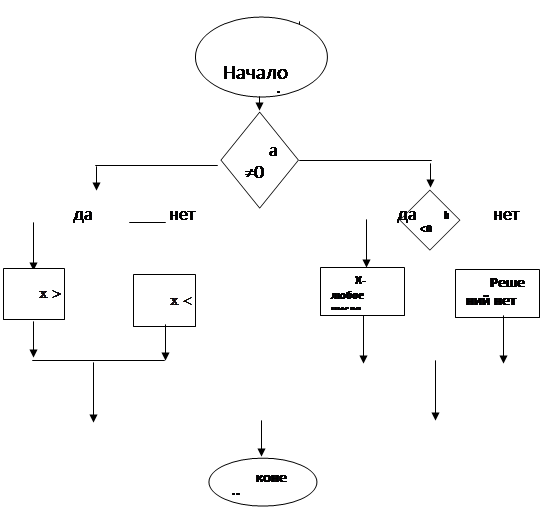
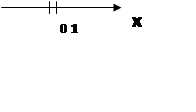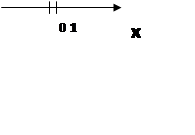Этапы изучения алгоритма в школе
да нет
 |
да
 |
|
Третий этап может быть очень разнообразным. Всё зависит от уровня знаний и умений учащихся. Но в любом случае надо начать с элементарных задач, а уже после формирования навыка решения линейных неравенств первой степени с одной неизвестной у учащихся.
Этап (актуализация знаний)
а) Изобразите на координатной прямой промежутки, соответствующие неравенствам:
х≥3,
x<-5,
x≤2
b)
–1.5≤x≤4,
2<y<6.1,
-3<z ≤ 9.2
c) Запишите неравенства, соответствующие ппромежуткам:
[2;+ ∞)
(-3;+ ∞)
(-∞;4)
(-5;3]
[-6;8]
(-∞;+∞)
2) Найдите пересечение промежутков
(1;8)∩(5;10)
[-4;4]∩ [-6;6)
(-∞;10) ∩ (-∞;6]
3) Найдите объединение промежутков
[7;10] и (-3;5]
[3;+] и (8;+)
(-;3] и (-5;16]
Запишите в виде неравенства утверждения
сумма чисел х и 17 больше 18;
разность чисел 13 и х меньше 2;
произведение чисел 17 и х не меньше 3;
удвоенная сумма чисел х и (-3) не больше 2;
полусумма чисел х и 3 не больше их произведения;
удвоенное произведение чисел х и (-4) не меньше их разности
5) Заполните пустые места таблицы
|
Неравенство |
Изображение решения |
Запись решения | |||
|
3<x<6 |
  |
(3,6) | |||
|
-2≤x≤4 |
|
… | |||
|
7<x≤10 |
|
…;10] | |||
|
…x<5 |
|
[-3;… | |||
|
… |
|
[4;+∞) | |||
|
-4<x…3 |
|
… |
Материалы по педагогике:
Диагностика умственных способностей
старших дошкольников
Изучив теоретические и методические аспекты данной литературы этой проблемы, мы перешли к практической части; определили цель и задачи: 1. Выявить условия эффективности развития умственных способностей старших дошкольников. 2. Провести диагностику уровня развития умственных способностей детей. 3. П ...
Мотивация учебной деятельности и поведения младших школьников
В школе есть ряд проблем, которые относят к старым, традиционным, то есть и те, с которыми неизбежно приходиться мириться. Проблема мотивации справедливо может быть отнесена к их числу. Учителя школы озабочены тем, что большинство детей относятся к учебе совершенно безразлично. От них часто можно у ...
Психолого-педагогические особенности подросткового возраста
Каждый возраст хорош по-своему. И в то же время, в каждом возрасте есть свои особенности, есть свои сложности. Не исключением является и подростковый возраст. Подростковый возраст – период жизни человека от детства до юности в традиционной классификации (от 11–12 до 14–15 лет). В этот короткий по а ...